En el triángulo y el ángulo , determinar el valor del lado y el valor de los ángulos y .1. Qué es la Física?
2. Qué pretende la Física?
3. Cuáles son las partes en que se divide la Física Mecánica?
4. Qué estudia cada una de las partes en que se divide la Física?
5. Cuáles son los cinco sistemas de unidades que se utilizan para el estudio de la Física Mecánica?
6. Cuáles de los cinco sistemas de unidades se utilizaran en el desarrollo de este texto?
7. Qué utilizó Galileo para medir el periodo de oscilación de un péndulo?
8. A qué hace referencia el concepto de longitud?
9. Qué es el Área?
10. Qué es Volumen?
11. Cuál es el concepto de Velocidad?
12. Qué es la aceleración?
13. Qué es la masa?
14. De qué está compuesta la materia?
15. En el sistema de unidades F.P.S. cuál es la unidad para la masa y cual es su equivalente en Kilogramos?
16. Cuál es el concepto de Fuerza?
17. Cuál es el modelo matemático de Newton para la Fuerza?
18. Cuál es la unidad para la fuerza en el Sistema internacional y en el sistema F.P.S.?
19. En el Sistema Internacional a qué equivale un Newton (N)?
20. En el Sistema F.P.S. a qué equivale una Libra (Lb)?
1. En un triángulo rectángulo los valores de los catetos son 12ft y 5ft respectivamente, determinar el valor de la hipotenusa y comprobar por Pitágoras el valor de los catetos.
2.
En el triángulo a=5ft c=12ft y el ángulo β=60°, determinar el valor del lado b y el valor de los ángulos α y γ.
3. Un obrero debe subir una distancia a y bajar una distancia b con una carretilla por una rampa que tiene una inclinación al subir de 30∘ y al bajar de 37∘. Si se sabe que la base c de la rampa mide 30m, Calcular la longitud de cada tramo de la rampa y el ángulo γ entre los dos tramos.
4. Se desea calcular la distancia d entre dos edificios. El analista se encuentra en un punto A. Los datos que tiene son las distancias de él respecto a los edificios, 180ft y 210ft, respectivamente, también sabe que el ángulo α formado por los dos edificios y su posición actual es de 39.40° ¿Qué distancia hay entre los dos edificios?
5. La distancia d entre los puntos A y B es de 20Km. Los ángulos de elevación de un globo G con respecto a dichos puntos son de 45° y 60°. ¿A qué altura h del suelo se encuentra el globo?
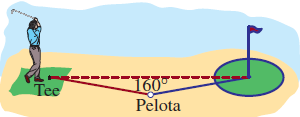
6. La distancia del tee al green de un determinado hoyo de golf es de 370 pies. Un golfista realiza su primer golpe y coloca la bola a 210 pies del hoyo. Desde el punto donde quedó la pelota, el golfista mide un ángulo de 160∘ entre el tee y el green. Obtenga el ángulo de golpeo desde el tee medido desde la línea punteada que va del tee al green y la distancia donde está la bola.
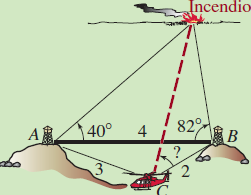
7.Dos torres vigía están situadas en las cumbres de las montañas A y B, a 4 millas de distancia. Un equipo de bomberos en helicóptero está en un valle en el punto C, a 3 millas de A y a 2 millas de B. Usando la línea entre A y B como referencia, un vigía ve un incendio en un ángulo de 40∘ de la torre A, y a 82∘ de la torre B, como se muestra en la figura. ¿A qué ángulo, medido a partir de CB, debe volar el helicóptero para dirigirse hacia el incendio?
8. En la figura se ilustra un funicular que lleva pasajeros de un punto A, que está a 1.2 millas de un punto B en la base de una montaña, a un punto P en la cima de la montaña. Los ángulos de elevación de A y B dirigidos hacia P son 21∘ y 65∘, respectivamente.
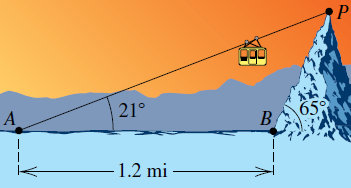
a. Calcule la distancia AP.
b. Calcule la altura de la montaña.
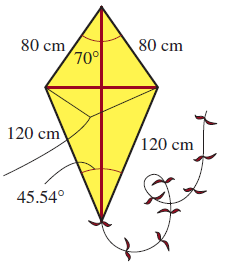
9. Para la cometa que se muestra en la figura, determine las longitudes de las dos cañas que se requieren para los soportes diagonales.
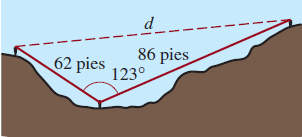
10. Desde el suelo de un cañón se necesitan 62 pies de soga para alcanzar la cima de la pared del cañón y 86 pies para alcanzar la cima de la pared opuesta, como se muestra en la figura. Si las dos sogas forman un ángulo de 123∘ , ¿cuál es la distancia d desde la cima de una pared del cañón a la otra?
11.Un bote pesquero mercante utiliza un equipo de sonar para detectar un banco de peces a 2 millas al este del bote. El banco de peces se desplaza en la dirección N51∘W a razón de 8hmi, como se muestra en la figura.
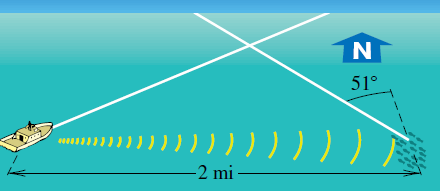
a. Si el bote navega a 20hmi, calcule, la dirección a la que debe dirigirse el bote para interceptar el banco de peces.
b. Encuentre, el tiempo que tardará el bote en llegar a los peces.
c. Determine la distancia dP que recorre el banco de peces en éste proceso.
d. Determine la distancia dB que recorre el bote.
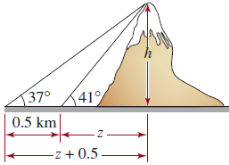
12. Un topógrafo usa un instrumento llamado teodolito para medir el ángulo de elevación entre el nivel del piso y la cumbre de una montaña. En un punto, se mide un ángulo de elevación de 41∘. Medio kilómetro más lejos de la base de la montaña, el ángulo de elevación medido es de 37∘, como se muestra en la figura. ¿Qué altura tiene la montaña?
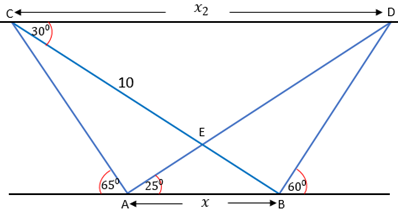
13. Hallar el valor de x y x2 si se sabe que la distancia CE=10 y que los segmentos de recta CD y AB son paralelos.
14.Dos observadores desde puntos distintos, ven dos globos, que están en el mismo plano vertical en el cual están ellos. La distancia entre los observadores es de 1 Kilometro.
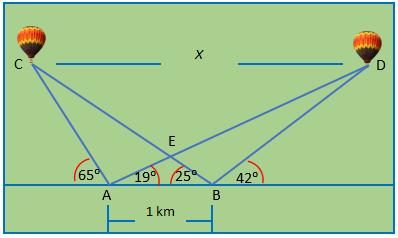
a. Hallar la distancia x entre los dos globos.
b. Determine la altura del globo en C medida desde el suelo.
c. Determine la altura del globo en D medida desde el suelo.